Moment generating function of a discrete distribution
Emin Gabrielyan /
2010-09-22
Moment
generating function of a discrete distribution
Moment
generating function of a uniform distribution
Moment
generating function of a degenerate distribution
Moment
generating function of a discrete distribution with two possible values
The
moment generating function of a distribution with multiple discrete values
The
discrete distribution behind the moment generating function of this task
The task
For a random variable X
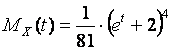
Find
![]()
Moment generating function of a uniform distribution
Let us compute the moment generating function of a uniform distribution
By definition of the uniform probability density function:
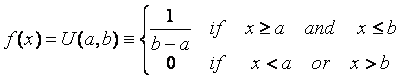
By definition of the moment generating function:
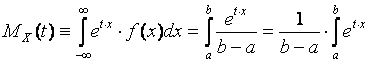
By derivative chain rule:
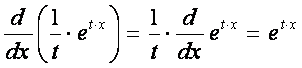
Therefore:
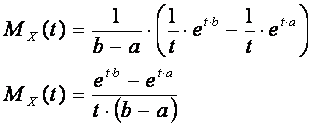
Moment generating function of a degenerate distribution
Let us compute the moment generating function of a degenerate distribution, a discrete distribution with only one possible value.
![]()
The moment generating function is the extreme case of a uniform distribution:

Therefore:
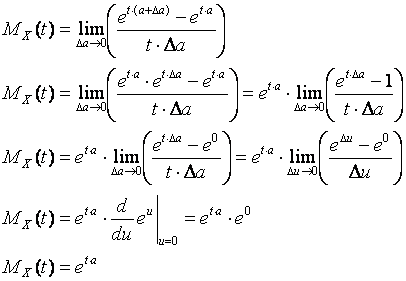
Moment generating function of a discrete distribution with two possible values
A discrete distribution with two possible values can be represented as follows
![]()
Where
![]()
The moment generating function of the random variable with two possible values is:
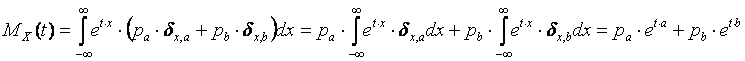
The moment generating function of a distribution with multiple discrete values
Similarly to the moment generating function with two values, for a discrete distribution with N possible values:
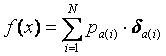
Where

The moment generating function is written as follows:
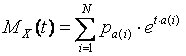
The discrete distribution behind the moment generating function of this task
The moment generating function of the task is shown below:
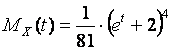
Let us open the parenthesis:

As 1+8+24+32+16=81
Then the condition of the sum of probabilities is respected:

Therefore we are dealing with a random variable distribution over the 5 discrete values:
4, 3, 2, 1, and 0
With the following probabilities:
1/81, 8/81, 24/81, 32/81, and 16/81
The answer
The probability, that:
![]()
Is equal to 24/81 + 32/81 + 16/81 = 72/81 = 8/9
The answer is 8/9
References:
http://en.wikipedia.org/wiki/Moment-generating_function
The moment generating function of a uniform distribution [xls]
* * *