ARON of Capillary Routing

To evaluate the friendliness of the capillary routing toward tolerant media streaming we must measure the ARON values of routings suggested by each capillary layer. There is no need to compare the capillary routing with any single path routing suggestion, which is too bad, since no FEC may save the media stream if the link failure time (or the failure detection and recovery time) is longer than the media buffering time. And so, as a reference for the comparison, we use the first layer of the capillary routing (with removed critical links if any). The first reference layer is a routing with a load balance of the main mass of the flow. The routing of the first layer has the footprint of the max-flow solution. The first layer of the capillary routing is similar to the path diversity schemes discussed in [Nguyen03], [Ma03], [Qu04] and [Tawan04].

To evaluate the overall performance of the capillary routing technique, rather than to measure the performance of a particular routing example, we need many network samples. Thus we can take the average ARON rating for all network samples in the test-bed set. First we suggest the first layer routing individually to each network sample of the test-bed set and we obtain thus the average ARON rating for all routing suggestions of the first layer. Then we compute the second layer routing individually for each network sample in the set and we obtain therefore the set’s average ARON rating for the routing suggestions of the second layer. We measure similarly until the average ARON for the routings of the 10^th capillary layer. We obtain thus an overall performance figure toward the layers of the capillary routing for the entire set of network samples.

In the figure below we have seven test-beds, each one with 42 network samples. For each test-bed we have a curve of the average ARON, which decreases as the capillary routing layer increases from 1 thru 10. Instead of one curve there are several curves for ARON, each following the tendency of decrease with the increase of the layer. These curves represent 16 different media streams with various values t of permanently maintained constant tolerance to losses.

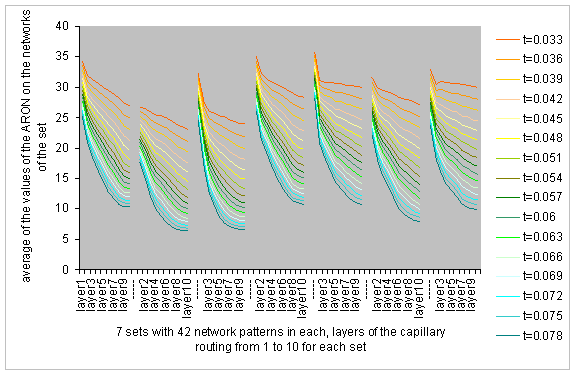
For example the permanently maintained constant tolerance of a VOIP stream, using the medium complexity (g729r8) or high complexity codecs (g723r53 and g723r63), is from 8% to 11% of packet losses (with a payloads from 20 up to 60 bytes). Although the video stream is more sensible to losses, it also is equipped with an internal tolerance resulting from the passive error concealment when the motion level is not very high and from an internal weak FEC code. The permanent tolerance of any application (even with zero initial tolerance like in a file transfer) can be obtained by constantly maintaining at the source a proper amount of the redundant data. Logically, the ARON curve of the media stream is shifted down by every unit of the added permanent tolerance. At the same time it is interesting to observe that the presence of a permanent tolerance in the media stream also stresses the efficiency gain achieved by the deeper layers of the capillary routing.

The network samples for the test-beds are obtained from a random walk Mobile Ad-hoc Network (MANET) on a rectangular space (Several other authors studied reliable multi-path routing in MANET: [Tawan04] or [Ma03] and [Ma04] using a concept of hop-by-hop packet recovery assuming regenerating nodes). Initially our nodes are randomly distributed on the rectangular area, and then at every timeframe they move according to a random walk algorithm. If two nodes are close enough (are within the coverage range) then there is a link between them. In the above example, there are 115 nodes and 300 timeframes, and therefore 300 various network samples. These 300 patterns are broken into 7 sets represented on the above chart. The number M of media packets per each transmission block is 20 and the desired decoding failure rate DER is . In AMR codec or in g729r8 codec with a 20 byte payload the sample duration is 20 ms, thus 20 packets in the transmission block requires a playback buffer of 400 ms. In real-time voice communication the human perception may tolerate 500 up to 600 ms delay [Padhye00].

In the example below the network consists of 120 nodes and there are 150 timeframes of the random-walk ad-hoc network. The 150 different network samples are broken into four sets.

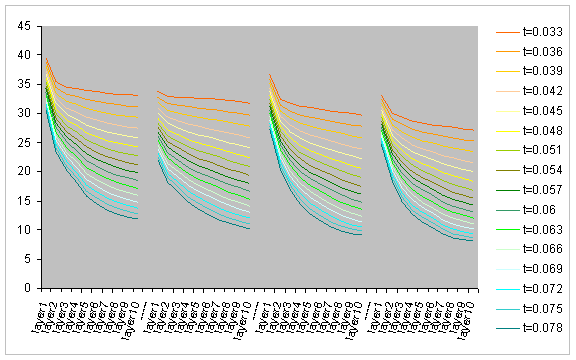
The media streaming parameters are identical to those of the previous example (, ).

For the same set of the network samples we may wish to see how performs ARON assuming Shannon capacity. As expected ARON computed with the Shannon capacity (see the chart below) assumption has much lower values compared with “true” ARON assuming the MDS encoder and the binomial probabilities of the failure.

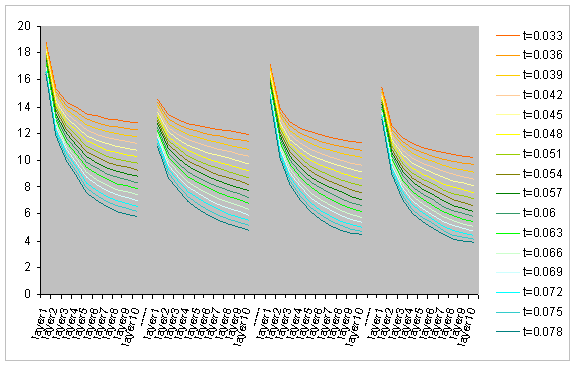
Below are the both curves on one chart, “true” ARON curves above and the curves derived from the Shannon capacity below.

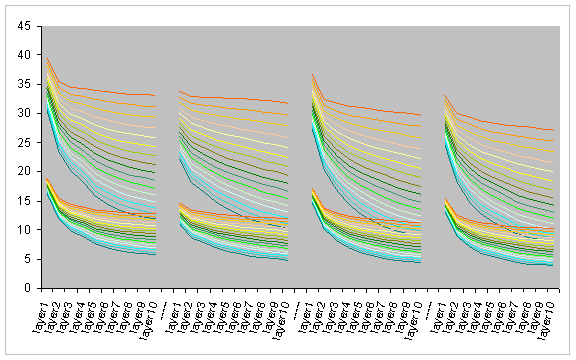
It remains us to show yet another chart, which does not precisely represent the ARON values but other similar values which characterizes rather the encoder effort during the failures than during the whole communication time. Recall that the formula below gives us the number of the redundant packets that the sender will be obliged to additionally send, due to the network failures, during the communication period T:

Where:

- s is the failure periodicity of a single link (the same for all links), i.e. the link fails approximately every s seconds

- d is the duration of a single failure

- B is the block transmission rate (which is supposed to be constant, while the packet transmission rate may rise due to adaptive increase of the redundant packets in the block)

ARON, represented by the below equation, is the proportionality coefficient for the amount of redundancy transmitted during the communication time.

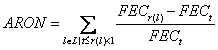
By spreading the communication footprint (when we increase the layer of the capillary routing) we increase the frequency of link failures, however the overall value of ARON goes down, since the effort necessary to recover an increased number of failures of lightly loaded links is lower the effort needed for the recovery of a few failures but of highly loaded links. In [Nguyen03] the author used RS(30,23) code and studied the routing of media through an OSPF route (with 10 ms failure time per 1 second of good time) altered with a longer route of five times lower quality (50 ms failure time). It was shown that the double-path routing, even if involving a bad route, is better the single shortest path routing. According to the author, this suggests that if there exists a redundant path which is not “nearly” as good as the default path between sender and receiver, then it is still advantageous to deploy the path diversity scheme.

However one may not be interested in the total amount of the sender’s encoding effort during the whole communication time, but in the average effort required from the encoder only during the failure time. The average effort expected from the sender whenever the receiver reports a failure (by observing missing packets) may have higher significance for a particular application and can be computed as follows:

The two charts below show the progress of this value, in the linear and the logarithmic scales, as the layers of the capillary routing rise. We can observe that the average recovery cost per link failure decreases more than 10 times from the first layer of the capillary routing through its 10^th layer.

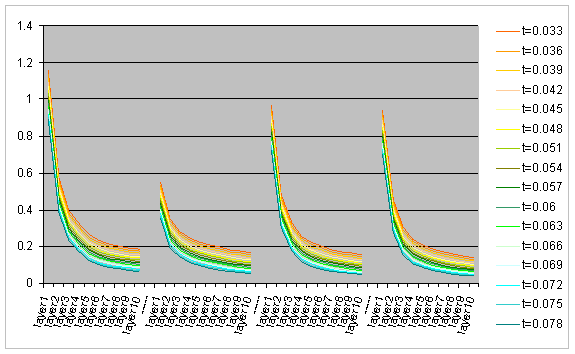
Average cost of single link failure recovery in the linear scale for the first 10 layers of the capillary routing

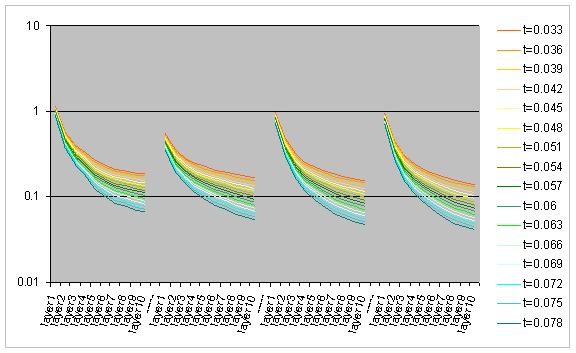
Average cost of single link failure recovery in the logarithmic scale for the first 10 layers of the capillary routing