Emin Gabrielyan /
2010-09-22 < 2010-09-22 < 2010-09-22 < 2010-09-22
Moment
generating function of a discrete distribution
1. The logarithm of the moment
generating function
2.1. The moment generating function of a
uniform distribution
2.2. The moment generating function of a
degenerate distribution
2.3. The moment generating function of a
discrete distribution with two possible values
2.4. The moment generating function of a
distribution with multiple discrete values
2.5. The discrete distribution behind
the moment generating function of this task
1. The logarithm of the moment generating function
1.1. The task
Let
![]()
be the moment generating function of X, and define
![]()
Show
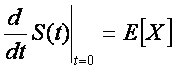
1.2. Proof
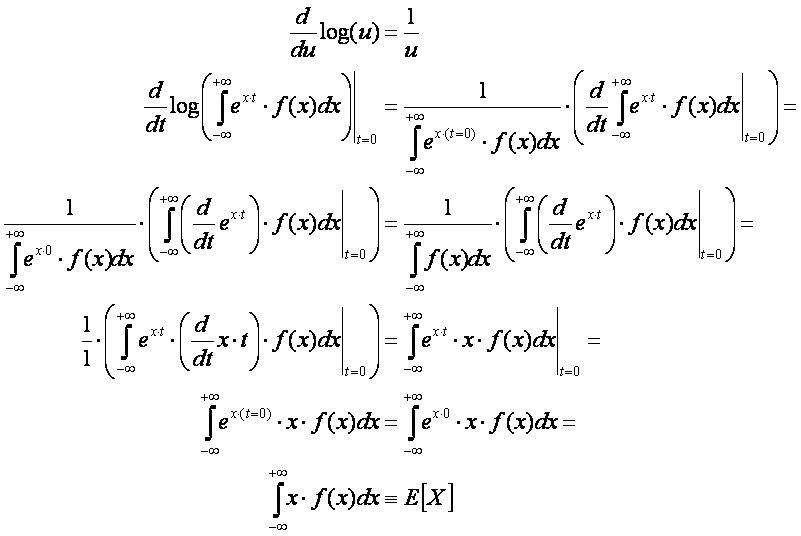
1.3.
The task
Let
![]()
be the moment generating function of X, and define
![]()
Show
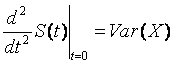
1.4. Proof
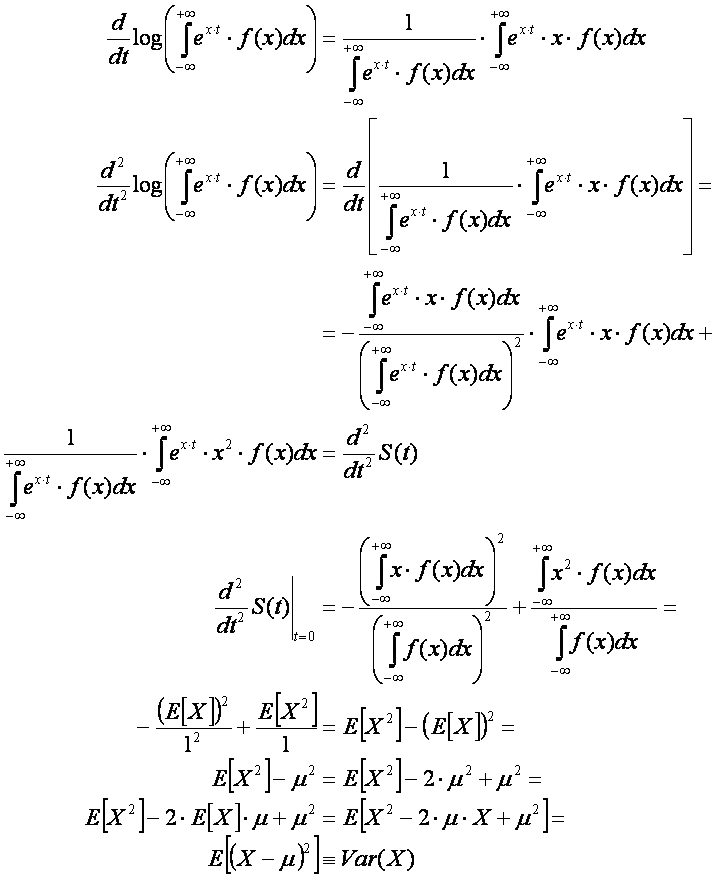
1.5.
References
http://en.wikipedia.org/wiki/Variance
http://en.wikipedia.org/wiki/Derivative
2. The task
For a random variable X
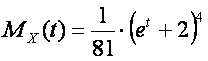
Find
![]()
2.1. The moment generating function of a uniform distribution
Let us compute the moment generating function of a uniform distribution
By definition of the uniform probability density function:
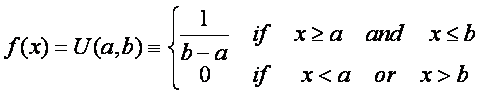
By definition of the moment generating function:
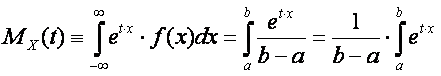
By derivative chain rule:
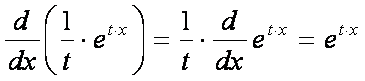
Therefore:
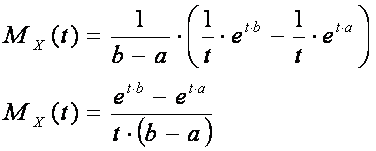
2.2. The moment generating function of a degenerate distribution
Let us compute the moment generating function of a degenerate distribution, i.e. a discrete distribution with only one possible value.
![]()
The moment generating function of a degenerate function is the extreme case of the uniform distribution with the upper bound infinitively approaching to the lower bound.
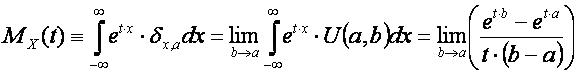
Therefore:
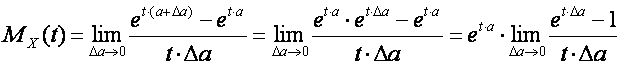
Replace
![]()
By
![]()
The expression of the limit in the equation becomes the definition of the derivative of the exponential function at the point 0.
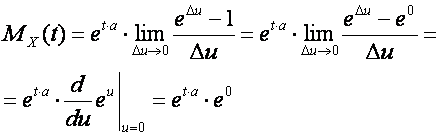
And finally, we write the moment generating function of the degenerate distribution:
![]()
2.3. The moment generating function of a discrete distribution with two possible values
A discrete distribution with two possible values can be represented as a weighted sum of two degenerated distributions:
![]()
Where
![]()
The moment generating function of the random variable with two possible values is:
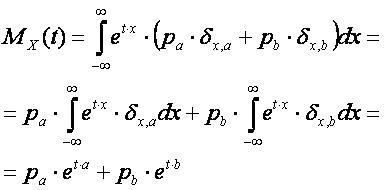
2.4. The moment generating function of a distribution with multiple discrete values
Similarly to the moment generating function with two possible values only, we can represent the moment generating function also for a discrete distribution with N possible values:
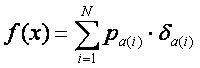
Where
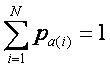
The moment generating function now can be written as follows:
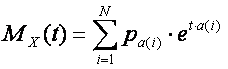
2.5. The discrete distribution behind the moment generating function of this task
The moment generating function of this task is shown below:
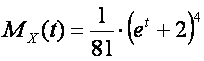
Let us open the parenthesis:
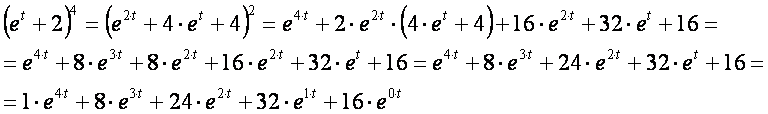
As 1+8+24+32+16=81, the condition of the sum of probabilities is respected:
Therefore we are dealing with a random variable distribution over the 5 discrete values:
4, 3, 2, 1, and 0
With the following probabilities:
1/81, 8/81, 24/81, 32/81, and 16/81
The probability density function corresponding to this task is the following:
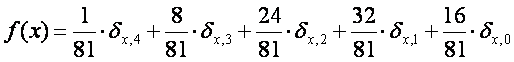
2.6. The answer
The probability, that:
![]()
Is equal to 24/81 + 32/81 + 16/81 = 72/81 = 8/9
The answer is 8/9
2.7. References
http://en.wikipedia.org/wiki/Moment-generating_function
The moment generating function of a uniform distribution [xls]
http://switzernet.com/people/aram-gabrielyan/public/100922-moment-gen-discrete-prob/
http://mirror2.switzernet.com/people/aram-gabrielyan/public/100922-moment-gen-discrete-prob/
The task source [pdf], [eml], [mht]
* * *